
Photo by Alina Grubnyak on Unsplash
Let's Hash It Out
Using Merkle Trees to Synchronize Data in Distributed Systems
Recently, I came across a rather fun and foundational problem dealing with peer-to-peer (P2P) communication and synchronization, and it got me thinking not only about solutions, but also applications. While numerous data layers are offered as a managed service at this point, there are still plenty that are not (or not sufficiently) and there are many of us that either want to work on the underlying technology or at least be knowledgeable of it. Data replication and sharding, distributed and/or decentralized applications, and more make use of P2P communication for synchronization, so this is a good problem to dive into and understand better.
The Problem Statement
The problem can be summarized as:
Given two peers in a P2P network, each possessing a set of strings, devise a way for each to end up with the union of their two sets that is efficient in terms of bandwidth and network calls.
The statement of the problem is intentionally vague, specifically because when this problem rises in practice the machine resources and additional constraints will vary. For this discussion, we will make the following assumptions
- Both peers already know the address of the other (no need for discovery)
- Each peer has sufficient memory to hold the strings and additional data (if needed)
The Easy (suboptimal) Solution
The easy thing to be done here is to have each peer send the other all of the data it possesses, and then they independently deduplicate their original set and the received set so that they each have the union. This would work, and when first implementing a solution this may be tempting, especially if the intersection of each peer's set is expected to be of low cardinality. But, we can do better... we just need to look at a data structure called a Merkle Tree. Let's review that, first!
The Merkle (or Hash) Tree
Merkle trees are used heavily in numerous domains such as blockchain, P2P networks, git, Nix, and multiple distributed data stores like Cassandra and Dynamo. The key concept is that of building a tree of hashes in a bottom-up method, as shown in this image (Source):
Many applications use binary trees, but the maximum number of leaves and whether to allow partial/incomplete branches is not dictated and can be decided by the implementor. For the remainder of this article we'll use a perfect binary tree.
The algorithm for comparing two Merkle trees is simple and recursive
- Starting at the root, do a hash compare
- If the root hashes are equal, we're done!
- If not, request the roots of the child trees and compare them as a new root node (then repeat for each hash for which a match is not found)
Now, let's walk through this using a simple example!
A Simple Example
Suppose we have two instances, A and B, that are peers in a P2P network, know one another's address, and have the following sets of strings:
| A | B |
| this is a string | some string!@#$ |
| some string!@#$ | this is a string |
| my special note | don't panic! |
| but can you read this? | my special note |
In this toy example each set differs from the other by only 1 string (for a total of 2 strings not in the intersection), but this will suffice for walking through how Merkle trees solve our problem. Now, let's first hash each of these strings (using SHA256) so that we can begin building our tree (throughout this we'll replace the center 52 characters with the ellipses, ...):
| A | B |
| bc7e8a...1fffc6 | ab5384...6c5f1d |
| ab5384...6c5f1d | bc7e8a...1fffc6 |
| 7a8be3...965f51 | c3651c...cae16b |
| 573998...57e8d5 | 7a8be3...965f51 |
If we proceeded from here to building a tree using the ordering of the list as provided, this wouldn't be as advantageous. So, we want to first sort the hashes, and will choose ascending order.
After building the full tree, we have the following trees for peers A and B, with the green nodes indicating a hash match was found (and thus we don't need to check any children of that node)
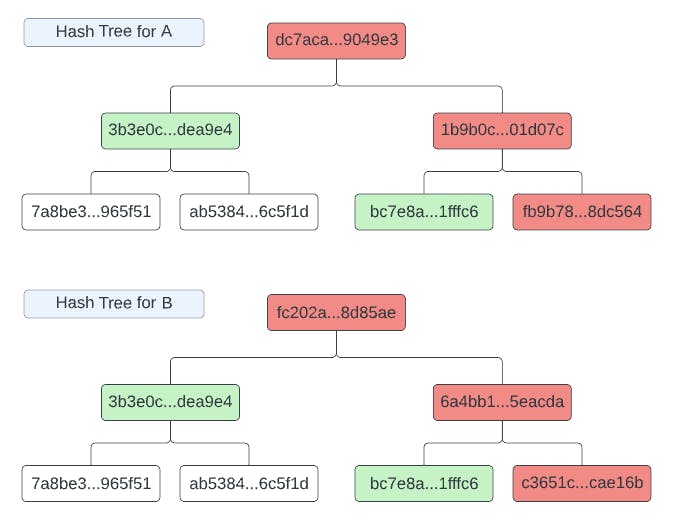
If we look at these two trees, we see that we need to do comparisons on the root (level 0), the two nodes in level 1, and then only the 2 leaves under the righthand node in level 2 (because we can early exit on the left side node in level 1). At such a small scale, it may seem to be no better than sending all strings, but if we instead had tens of thousands of strings (as is the case in blockchains and distributed databases), this algorithm has proven to be significantly better than virtually all other methods.
Conclusion
Merkle trees are simple and efficient, and can be used for a number of purposes. Whether designing a P2P network for a new application, looking for a way to detect and replace corrupted bytes of data, or even trying to support local subgraph synchronization to speed up distributed knowledge graph querying, Merkle trees can help.

